Binomiales Repräsentationstheorem – Part I: Keine Zinsen beschreibt die Bewertung von unsicheren Zahlungen mittels Martingalen und wie diese Bewertung mit Arbitragefreiheit zusammenhängt. Mit Hilfe der EXCEL-Datei können die für das Beispiel durchgeführten Berechnungen selbständig nachvollzogen und erweitert werden. Vor einigen Jahren, ungefähr 2014, schrieb ich die erste Version des Artikels und entschied mich aus didaktischen Gründen, die Zinsen auf Null zu setzen. Tatsächlich gingen in den Folgejahren die Zinsen nicht nur auf Null, sondern sogar in den negativen Bereich.
Die EXCEL-Datei
Mit der downloadbaren Datei brpt können die im Artikel beschriebenen Sachverhalte auf eine einfache Art und Weise nachvollzogen werden.
In den Zeilen 3 – 11 können die Auszahlungsstruktur und Preise für die Aktie und das Derivat spezifiziert werden. Der Wert des Derivats kann ganz beliebig gewählt werden. Im Beispiel ist dieser mit f=4 (Zeile 8) absichtlich nicht der arbitragefreie Wert.
In der Zeile 13 wird Φ berechnet, und zwar auf Grundlage des vorgegebenen Derivatwertes f, der beliebig sein kann.
In den Zeilen 16 und 17 werden auf Grundlage von Φ die Auszahlungen des Derivats berechnet.
Man sieht hier, dass die Differenz zwischen den Auszahlungen bereits korrekt ist, aber die Höhe der Auszahlungen nicht identisch mit denen des Derivat ist, siehe Abbildung 1.
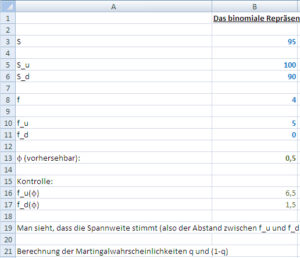
EXCEL, Abbildung 1
In der Zeile 26 werden die Martingalwahrscheinlichkeiten aus der Struktur (S, S_u und S_d) berechnet. Damit kann ein Erwartungswert für das Derivat berechnet werden, siehe Zeile 30. Setzt man diesen Wert in Zeile 8 für f ein, sieht man, dass jetzt nicht nur die Spannweite, sondern auch die Lage der mit Φ berechneten Auszahlungen f_u(Φ) und f_d(Φ) stimmen, siehe Zeilen 16 und 17, siehe Abbildung 2.
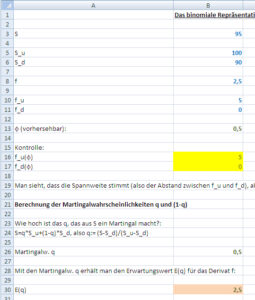
EXCEL, Abbildung 2
Natürlich kann man in die Zelle B8 „+B30“ zu schreiben. Damit hat man immer den „korrekten“ Wert für das Derivat in B8 stehen. Ab Zeile 34 folgt die Replikationsstrategie. Die Anzahl der Aktien im Portefeuille beträgt Φ, Zeile 40.
Der Preis wird in Zeile 42 berechnet. Im Beispiel wird eine halbe Aktie für 47,5 gekauft. Die Kreditaufnahme errechnet sich aus der Differenz zwischen Wert der Aktienposition und dem Wert des Derivats, siehe Zeile 46, im Beispiel wird ein Kredit in Höhe von 45 aufgenommen, damit hat man für das Portefeuille bestehend aus einer halben Aktie und einem Kredit in Höhe von 45 Geldeinheiten 2,5 Geldeinheiten ausgegeben. In Zeile 50 und 51 sieht man wie das Portefeuille aus den Aktien und der Kreditaufnahme, die gleichen Auszahlungen wie das Derivat aufweist, siehe Abbildung 3.
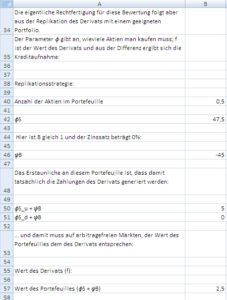
EXCEL, Abbildung 3
Da der Wert dieses Portefeuilles gleich dem mit den Martingalwahrscheinlichkeiten berechneten Erwartungswert ist, ist dies auch der korrekte – nämlich arbitragefreie – Wert des Derivats.
